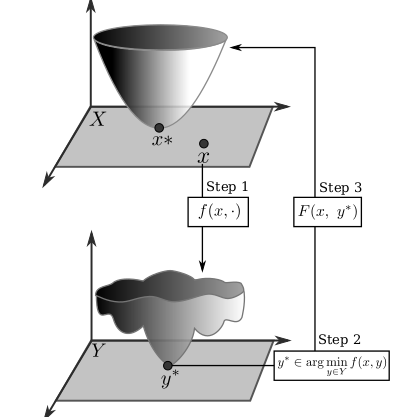
Bilevel Optimization is a challenging class of problems where the performance of an upper level “leader” problem is realizable only if the decision vector of a nested lower level “follower” problem is at its optimum. Alternatively, it can also be defined as an optimization problem which has another optimization problem as a constraint. Several real-life problems are hierarchical in nature and suited for modelling as bilevel optimization problem. These include (but are not limited to) transportation, policymaking, supply-chain management, economics, engineering design, defense strategies, cyber-security, etc. This hierarchical nature of the problem induces several unique challenges, such as:
- Exorbitant numbers of function evaluations are required for solving the problem, since evaluation of each upper level solution requires optimization of a lower level problem. It is proven that even if both levels of the problem are linear, the resulting problem is NP-hard.
- The leader and follower problems may be uncooperative, posing a severe difficulty for the ranking techniques used in evolutionary methods
- Further complexity is induced when the upper/lower level problems contain multiple objectives and/or constraints.
- Performance characterization and benchmarking of algorithms for such problems is not straightforward, since a suboptimal solution at lower level may result in a better-than-optimal solution at upper level.
Purpose of the TF
A number of studies exist in the classical literature to solve bilevel problems, but they usually involve assumptions on or knowledge of mathematical properties of the involved functions, which may severely limit their application for problems that are highly nonlinear or black-box. Evolutionary/metaheuristic and hybrid methods offer a way forward to solve such problems. The interest in use of evolutionary techniques is relatively recent, but is gaining significant traction. This task force aims to intensify efforts towards development of powerful techniques to solve difficult bilevel problems currently intractable. Some of the channels include
- Building an online community for sharing latest developments and resources to advance the field
- Organization of special sessions and tutorials in major events and conferences such as CEC, EMO, PPSN, SSCI, etc.
- Organization of edited books and special issues in journals
- Collaborative projects and papers towards solving open challenges in the field
Technical Committee
Chair

Jesús-Adolfo Mejía-de-Dios
Vice-Chair

José-Fernando Camacho-Vallejo
Members
| Name | Institution | Country |
|---|---|---|
| Ankur Sinha | Indian Institute of Management Ahmedabad (IIMA) | India |
| Hemant Singh | University of New South Wales (UNSW) | Australia |
| Helio J.C. Barbosa | Laboratório Nacional de Computação Científica (LNCC) | Brazil |
| Jaqueline S. Angelo | Laboratório Nacional de Computação Científica (LNCC) | Brazil |
| Moriah B. Bostian | Lewis and Clarke College | USA |
| Fernando Camacho | Universidad Autónoma de Nuevo León (UANL) | Mexico |
| Abir Chaabani | Institut Supérieur de Gestion de Tunis (ISG) Tunis | Tunisia |
| Kalyanmoy Deb | Michigan State University (MSU) | USA |
| Eduardo Krempser | Oswaldo Cruz Foundation | Brazil |
| Hecheng Li | Qinghai Normal University | China |
| Xiaodong Li | RMIT University Melbourne | Australia |
| Pekka Malo | AALTO University | Finland |
| Jie Lu | University of Technology Sydney (UTS) | Australia |
| Guangquan Zhang | University of Technology Sydney (UTS) | Australia |
| Yuping Wang | Xidian University | China |
| Gerald Whittaker | Oregon State University (ORST) | USA |
| Tapabrata Ray | University of New South Wales (UNSW) | Australia |
| El-Ghazali Talbi | University of Lille | France |
| Jesús-Adolfo Mejía-de-Dios | Universidad Autónoma de Coahuila | Mexico |
